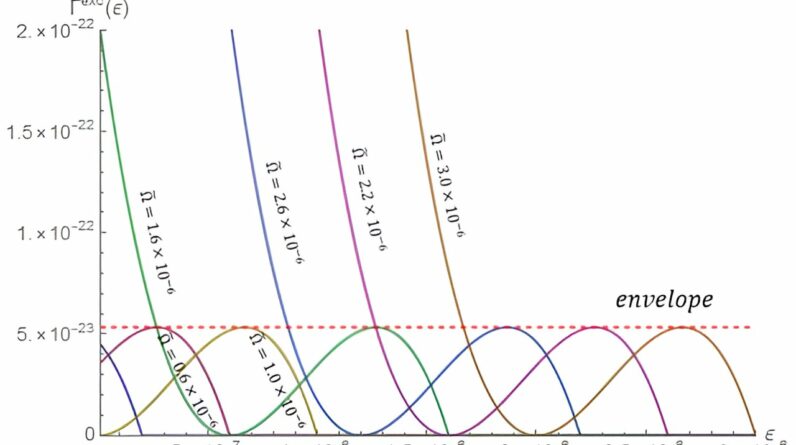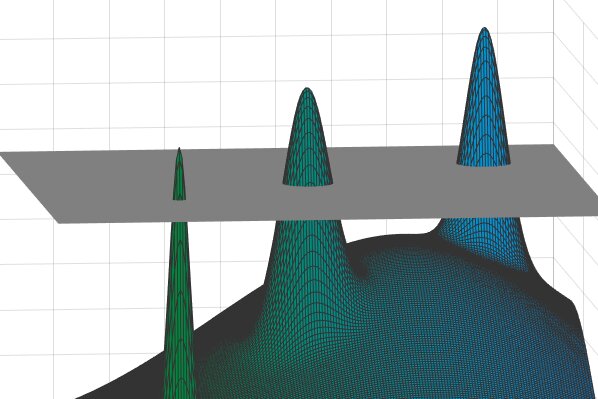
Em alguns casos, o diâmetro de cada pico será muito menor do que as distâncias entre os diferentes picos. Assim, se alguém escolhesse quaisquer dois pontos nesta vasta paisagem – isto é, duas “soluções” possíveis – eles estariam muito próximos (se viessem do mesmo pico) ou muito distantes (se retirados de picos diferentes). . Em outras palavras, haverá uma “lacuna” reveladora nessas distâncias – pequena ou grande, mas nada no meio. Crédito: David Jamarnik et al.
A ideia de que alguns problemas computacionais em matemática e ciência da computação podem ser difíceis não deve ser uma surpresa. Existe, de fato, toda uma classe de problemas para os quais se considera impossível resolver matematicamente. Abaixo desta categoria estão alguns problemas “mais fáceis” que não são bem compreendidos – e também podem ser impossíveis.
David Jamarnik, Professor de Pesquisa Operacional da MIT Sloan School of Management e do Institute for Data, Systems, and Society, concentra sua atenção na última categoria de problemas menos estudados, que são mais relevantes no mundo cotidiano porque envolvem Aleatória—Uma característica essencial dos sistemas naturais. Ele e seus colegas desenvolveram uma ferramenta poderosa para analisar esses problemas chamada de propriedade da lacuna sobreposta (ou OGP). Gamarnik descreveu a nova metodologia em um trabalho de pesquisa recente em Anais da Academia Nacional de Ciências.
P NP
Cinquenta anos atrás, o problema mais famoso da ciência da computação teórica foi formulado. P ≠ NP pergunta se há problemas envolvendo grandes conjuntos de dados cuja resposta pode ser verificada de forma relativamente rápida, mas que – mesmo trabalhando nos computadores mais rápidos disponíveis – levaria um tempo absurdamente longo para ser resolvido.
A conjectura P ≠ NP ainda não foi comprovada, mas a maioria dos cientistas da computação acredita que muitos problemas familiares – incluindo, por exemplo, o problema do caixeiro viajante – se enquadram nessa categoria incrivelmente difícil. O desafio no exemplo do vendedor é encontrar a rota mais curta, em termos de distância ou tempo, através de N cidades diferentes. A tarefa é facilmente gerenciada quando N = 4, pois existem apenas seis caminhos possíveis a serem considerados. Mas em 30 cidades, há mais de 1030 maneiras possíveis, e os números aumentam exponencialmente a partir daí. A maior dificuldade está em projetar um arquivo algoritmo Ele resolve o problema rapidamente em todos os casos, para todos os valores inteiros de N., os cientistas da computação estão confiantes, com base na teoria da complexidade computacional, que não existe tal algoritmo, confirmando que P ≠ NP.
Há muitos outros exemplos de tais problemas intratáveis. Suponha, por exemplo, que você tenha uma tabela de números enorme com milhares de linhas e milhares de colunas. Você consegue encontrar, de todas as combinações possíveis, o arranjo exato de dez linhas e 10 colunas de modo que suas cem entradas tenham a soma mais alta possível? “Nós as chamamos de tarefas de otimização, porque você está sempre tentando encontrar o maior ou o melhor – a maior soma de números, a melhor rota pelas cidades etc.”, diz Jamarnik.
Os cientistas da computação há muito perceberam que não é possível criar um algoritmo rápido que possa, em todos os casos, resolver problemas com a mesma eficiência da saga do caixeiro-viajante. “É provável que tal coisa seja impossível por razões bem compreendidas”, observa Jamarnik. “Mas na vida real, a natureza não gera problemas de uma perspectiva hostil. Ela não tenta frustrá-lo com um problema bem selecionado e mais desafiador concebível.” Na verdade, as pessoas geralmente encontram problemas em circunstâncias mais aleatórias e menos gerenciadas, e esses são os problemas que a Parceria de Governo Aberto visa resolver.
Picos e vales
Para entender do que se trata a Parceria de Governo Aberto, pode ser útil ver primeiro como a ideia se originou. Desde a década de 1970, os físicos estudam o vidro de spin – materiais que possuem propriedades de líquidos e sólidos que apresentam comportamentos magnéticos incomuns. A pesquisa em vidros de spin deu origem a uma teoria geral de sistemas complexos relacionados a problemas em física, matemática, ciência da computação, ciência dos materiais e outros campos. (Este trabalho rendeu a Giorgio Baresi o Prêmio Nobel de Física de 2021.)
Uma questão confusa que os físicos enfrentaram é tentar prever o estado de energia, particularmente as configurações de energia mais baixas, de diferentes estruturas de vidro giratório. A situação às vezes é retratada em uma “paisagem” de inúmeros picos de montanhas separados por vales, onde o objetivo é localizar o pico mais alto. Nesse caso, o pico mais alto na verdade representa o estado de energia mais baixo (embora se possa inverter a imagem e procurar o buraco mais profundo). Este acaba por ser um problema de otimização semelhante em forma ao dilema do caixeiro-viajante, Jamarnik explica: “Você tem esse enorme conjunto de montanhas, e parece que a única maneira de encontrar mais alto é escalando cada uma delas” – uma tarefa absurda semelhante para encontrar uma agulha no palheiro.
Os físicos mostraram que você pode simplificar essa imagem e dar um passo em direção a uma solução, cortando montanhas a uma certa altura predeterminada e ignorando tudo abaixo desse nível de corte. Você então deixará um grupo de picos proeminentes acima de uma camada uniforme de nuvens, com cada ponto desses picos representando uma solução potencial para o problema original.
Em um trabalho de pesquisa de 2014, Jamarnik e colegas observam algo anteriormente esquecido. Eles perceberam em alguns casos que o diâmetro de cada pico seria muito menor do que as distâncias entre os diferentes picos. Assim, se alguém escolhesse quaisquer dois pontos nesta vasta paisagem – isto é, duas “soluções” possíveis – eles estariam muito próximos (se viessem do mesmo pico) ou muito distantes (se retirados de picos diferentes). . Em outras palavras, haverá uma “lacuna” reveladora nessas distâncias – pequena ou grande, mas nada no meio. Jamarnik e colegas sugeriram que o sistema neste caso é caracterizado pela OGP.
“Descobrimos que todos os problemas conhecidos de natureza aleatória computacionalmente difícil têm uma versão dessa propriedade” – ou seja, o diâmetro da montanha no modelo esquemático é muito menor que a distância entre as montanhas, afirma Jamarnik. “Isso fornece uma medida mais precisa da robustez do algoritmo.”
Desvendando os segredos da complexidade do algoritmo
O advento do OGP pode ajudar os pesquisadores a avaliar a dificuldade de criar algoritmos rápidos para resolver problemas específicos. Já lhes permitiu “matematicamente [and] Ele descartou fortemente uma grande classe de algoritmos como potenciais concorrentes”, diz Jamarnik. Aprendemos, especificamente, que algoritmos estáveis - aqueles cuja saída não mudará muito se a entrada mudar um pouco – não resolverão esse tipo de problema de otimização. “Esse resultado negativo se aplica não apenas aos computadores clássicos, mas também aos computadores quânticos e, especificamente, aos chamados “algoritmos de otimização de aproximação quântica” (QAOAs), que alguns pesquisadores esperavam resolver os mesmos problemas de otimização. Agora, dados os resultados de Jamarnik e De acordo com as descobertas dos coautores, essas esperanças são temperadas pelo reconhecimento de que muitas camadas de operações serão necessárias para que os algoritmos do tipo QAOA sejam bem-sucedidos, o que pode ser tecnicamente desafiador.
“Se isso é uma boa ou má notícia depende do seu ponto de vista”, diz ele. “Acho que é uma boa notícia no sentido de que nos ajuda a desvendar os segredos da complexidade algorítmica e aumenta nosso conhecimento sobre o que está no reino da probabilidade e o que não está. É uma má notícia no sentido de que nos diz que esses problemas são difícil, mesmo que a natureza os produza, e mesmo que sejam gerados aleatoriamente”. Ele acrescenta que a notícia não é realmente surpreendente. “Muitos de nós esperávamos isso o tempo todo, mas agora temos uma base muito mais sólida para fazer essa afirmação.”
Isso ainda deixa os pesquisadores a anos-luz de conseguir provar que não existem algoritmos rápidos que possam resolver esses problemas de otimização em configurações aleatórias. Ter tal evidência forneceria uma resposta definitiva para o problema P NP. Ele diz: “Se pudermos provar que não podemos ter um algoritmo que funcione a maior parte do tempo, isso nos diz que definitivamente não podemos ter um algoritmo que funcione o tempo todo”.
Prever quanto tempo levará até que o problema P NP seja resolvido parece ser um problema intratável em si. Provavelmente haverá muitos picos para escalar e vales para atravessar, antes que os pesquisadores obtenham uma perspectiva mais clara da situação.
David Jamarnik, The Nested Gap Property: A Topological Barrier to Optimization Over Stochastic Structures, Anais da Academia Nacional de Ciências (2021). DOI: 10.1073/pnas.2108492118
Introdução de
Instituto de Tecnologia de Massachusetts
a citação: pesquisador desenvolve nova ferramenta para entender problemas computacionais difíceis e aparentemente intratáveis (2022, 10 de janeiro) Recuperado em 10 de janeiro de 2022 de https://phys.org/news/2022-01-tool-hard-problems-intractable.html
Este documento está sujeito a direitos autorais. Não obstante qualquer negociação justa para fins de estudo ou pesquisa privada, nenhuma parte pode ser reproduzida sem permissão por escrito. O conteúdo é fornecido apenas para fins informativos.